Trabajo mecánico y energía potencial gravitatoria
El trabajo mecánico que se necesita hacer para elevar un cuerpo a una cierta altura h, va a ser igual a la cantidad de energía potencial gravitatoria que almacena el cuerpo al alcanzar esa altura h.
A su vez si el cuerpo se suelta, cáera bajo la acción de la fuerza peso y desarrollará un trabajo que se pondrá de manifiesto por ejemplo aplastando un objeto que se encuentra en el piso.
Por ejemplo, como ya vimos para poder elevar una piedra por una pendiente hay que realizar un trabajo mecánico que le permita a la piedra almacenar energía potencial gravitatoria.
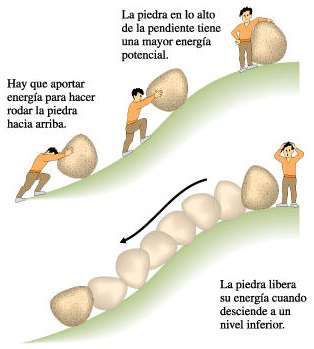
FIGURA 3-3 Para aumentar la energía potencial gravitatoria de la roca, la persona aplica una fuerza para poder desplazar la roca a una cierta altura. Es decir la persona realiza trabajo mecánico.
La fórmula que relaciona el trabajo mecánico con la energía potencial gravitatoria que almacena un cuerpo es:
![]()
Osea:
.gif)
W = trabajo mecánico medido en J.
Ep = energía potencial gravitatoria medida en J.
m = masa medida en kg.
g = aceleración de la gravedad medida en m/s2
h = altura medida respecto al piso (cero de referencia) en m.
Por ejemplo:
Calcula cuánto trabajo mecánico realiza una persona para elevar una caja de 50 kg a una altura de 12 m por sobre el nivel del piso.
Lees el problema y extraes datos e incógnita (recuerda que g = 9,8 m/seg2).
W = ?.
m = 50 kg.
h = 12 m.
g = 9,8 m/s2
Eliges la fórmula que te permite calcular la incógnita a partir de tus datos:
W = m . g . h.
Reemplazas los datos en la fórmula:
W = 50 kg . 9,8 m/s2 . 12 m.
Calculas el resultado numérico final y colocas la unidad en que se mide el trabajo mecánico:
W = 5880 J.
El trabajo mecánico que realiza la persona para elevar la caja es de 5880 J.