Representación en la recta numérica

Podemos representar los números naturales en una recta de la siguiente manera:

• trazamos una recta;
• elegimos un punto al que le hacemos corresponder el cero;
• elegimos un segmento cualquiera con un extremo en cero y en el otro extremo marcamos el número uno (1);
• luego transportamos consecutivamente el segmento y marcamos sucesivamente el número 2, el número 3, el número 4, ...

A continuación se muestra una recta numérica, que posee ocho segmentos equidistantes, es decir, todos separados a igual distancia. En ella podemos observar la ubicación de los primeros ocho números naturales.

 

 

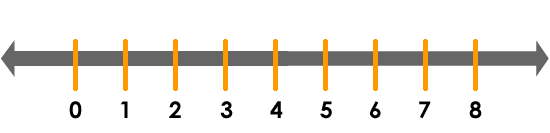
Para dibujar una recta numérica debemos asegurarnos de que la distancia que separa dos números sea siempre la misma, es decir, que los números sean equidistantes entre sí.

Por ejemplo, si la distancia entre 100 y 200 es de 2cm, la distancia entre 200 y 300 también deberá ser 2cm.

Cualquier otro número tiene que respetar esta escala, de manera proporcional, es decir por ejemplo el 150 estará justo a 1cm del 100 y del 200.

Gráficamente, un número natural es mayor que otro si al representarlo en la recta está situado más a la derecha  (está más lejos del cero).  

 

• Te invitamos a realizar una actividad sobre este tema, haciendo click aquí