Tablas de proporcionalidad inversa
En una fábrica de aceite se tiene que envasar 420 litros de aceite utilizando envases de distinta capacidad.
La siguiente tabla nos muestra como se relacionan la cantidad de envases utilizados según su capacidad.
| Capacidad del envase en litros | 1 | ||
| Cantidad de envases a utilizar | 840 | 315 | 420 |
Si observamos en la tabla, vemos que cuanto más grande es el envase, menos cantidad se necesitan.
Además, si multiplicamos las magnitudes obtenemos la constante de proporcionalidad inversa: k = ![]() . 840 =
. 840 = ![]() . 315 = 1 . 420 = 420
. 315 = 1 . 420 = 420
Analicemos como debes completar una tabla que muestra dos magnitudes inversamente proporcionales
|
Capacidad del envase en litros |
1 | 3 | |||
| Cantidad de envases a utilizar | 840 | 315 | 420 | 280 |
a) Para saber la capacidad del envase en litros para utilizar 280 envases debemos debemos ayudarnos con la constante de proporcionalidad que calculamos anteriormente:
![]()
En consecuencia la capacidad que de tener al envase es de un litro y medio.
b) Por otro lado, si sabemos que el envase puede contener 3 litro, realizamos el mismo procedimiento anterior es decir:
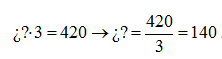
Por lo tanto la cantidad de envases a utilizar será de 140 litros.
Otra manera es aplicando la regla de tres simple:
A.

B.
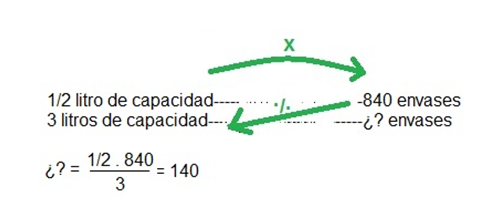
En síntesis, la tabla completa queda de la siguiente manera:
| Capacidad del envase en litros | 0,5 | 0,75 | 1 | 1,5 | 3 |
| Cantidad de envases a utilizar | 840 | 315 | 420 | 280 | 140 |