Aplicaciones

Las funciones lineales describen fenómenos en los que intervienen magnitudes directamente proporcionales.
La representación gráfica será una recta cuya pendiente nos informa de la rapidez de la variación de una magnitud con respecto a la otra y la ordenada en el origen nos informa sobre las condiciones iniciales.

EJEMPLOS:

1) Los taxis en la ciudad de San Luis tienen una tarifa que equivale a $5,25 la bajada de bandera y por cada minuto $0,50.

Si consideramos la variable independiente x al tiempo en minutos que se demora en realizar un viaje y la variable dependiente y al precio final que se paga, obtenemos la siguiente fórmula:

y = 5,25 + 0,50x

Es decir si el viaje demora 2 minutos se debe pagar y = 5,24 + 0,50. 2 = $6,24

Si una persona pagó $11,25 ¿Cuánto duró su viaje?

En este caso y = 11,25, si reemplazamos tenemos: 11,25 = 5,25 + 0,50x, ahora debemos "despejar" la x para poder responder la pregunta

11,25 - 5,25 = 0,50x

         6           = 0,50x

   6 : 0, 5       = x

   12              = x

Es decir demoró 12 minutos

 

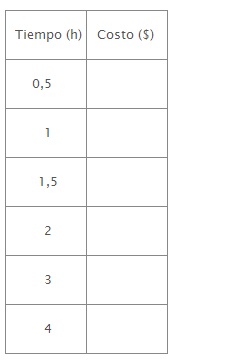
2)  Lucas es técnico en computadoras. Cuando le piden un servicio a domicilio, cobra un valor fijo de $50 y un adicional según el tiempo que le demore el trabajo, que calcula a razón de $20 la hora.