Resumen del módulo

Las operaciones para números: suma, resta, producto, división, son conocidas como operaciones aritméticas y  cuando se expresan en lenguaje matemático ciertas situaciones y representamos números y letras, estamos utilizando expresiones algebraicas.

Dentro de las expresiones algebraicas estudiadas en este módulo se trabajaron: las fórmulas, los polinomios, las identidades y las ecuaciones.

• Los polinomios son expresiones algebraicas en las que se utilizan únicamente las operaciones: suma, resta, multiplicación y exponentes naturales en las variables.
•  La identidad es una igualdad algebraica que es cierta para valores cualquiera de las letras que intervienen. 
• Una ecuación es una igualdad algebraica que es cierta solo para algunos valores de la variable.

 

 

Las ecuaciones de primer grado son aquellas en las cuales la incógnita se encuentra elevada al exponente 1. Recuerda los pasos para resolver ecuaciones en el enlace.

 

Las ecuaciones de segundo grado  son de la forma ax² + bx + c = 0. Éstas se resuelven aplicando la siguiente fórmula:

Si b² – 4ac > 0, hay dos soluciones

Si b² – 4ac = 0, hay una solución

Si b² – 4ac < 0, no hay solución

Es aquel sistema formado por dos rectas perpendiculares entre sí. El punto de corte de ambas rectas se llama origen de coordenadas. Además el plano queda dividido en cuatro regiones llamadas cuadrantes.

La recta Horizontal se llama eje de las abscisas y la simbolizamos con la letra x, y la vertical se llama eje de ordenadas y se simboliza con la y.

En este sistema se pueden representar puntos:

Para indicar la posición exacta de un punto, basta con indicar las unidades que ese punto se aleja del origen de coordenadas, tanto en sentido horizontal (eje x), como en sentido vertical (eje y).

Recorda que debes tener especial cuidado en respetar ese orden de representación, es decir, el valor del punto en el eje x y en el eje y, ambos separados por una “coma”. Por ejemplo, si nos indican que el punto “A” es el (2,3), quiere decir que ese punto “A” está separado dos unidades del punto de corte en el eje de abscisas y tres en el eje de ordenadas.

Una función es una regla que asocia dos conjuntos entre sí., tomando elementos de uno y a través de una regla devuelve otros.

 Ya sean relaciones entre conjuntos numéricos o no, siempre se cumplen los principios:

1. Todos los elementos o valores de la primera variable están relacionados con un elemento de la segunda variable.

2. A cada elemento o valor de la primera variable  le corresponde un único elemento de la segunda variable.

 Una función puede representarse mediante:

TABLA DE VALORES recoge los datos x e y  presentándolos en tablas verticales u horizontales.

UN GRÁFICO se construye a través de una tabla de valores o de su expresión analítica.

Un ENUNCIADO describe la relación entre variables mediante palabras.

La EXPRESIÓN ANALÍTICA es la expresión algebraica que relaciona las variables x e y, también se suele llamar Fórmula.

Una función de la forma f(x) = ax + b se conoce como una función lineal, donde a representa la pendiente (inclinación de la recta) y b representa la intersección de la recta con el eje y.

La representación gráfica de una función lineal es una recta.

Para graficar una función lineal existen dos formas para hacerlo:

• Utilizando una tabla de valores.
• Ubicando la ordenada al origen y usando el valor de la pendiente

Una función cuadrática es aquella que puede escribirse como una ecuación de la forma:

f(x) = ax² + bx + c

donde a, b y c (llamados términos) son números reales cualesquiera y a es distinto de cero (puede ser mayor o menor que cero, pero no igual que cero). El valor de b y de c sí puede ser cero.

En la ecuación cuadrática cada uno de sus términos tiene un nombre.

Así,

ax² es el término cuadrático

bx es el término lineal

c es el término independiente

La gráfica de una función cuadrática es una curva llamada parábola. Esta curva puede ser que se abra hacia arriba o hacia abajo.

Para construir la gráfica de una función cuadrática dada su fórmula, es posible construir a partir de los siguientes puntos:

Población: Conjunto finito o infinito de elementos, sobre los que vamos a realizar observaciones.

Muestra: Subconjunto finito de una población. El número de elementos que forman la muestra se denomina tamaño muestral.

Variable: es cada una de las características que pueden observarse de un elemento de la muestra.

 Las variables pueden ser clasificadas en dos grupos:  

a) Cualitativas: toman valores no numéricos. Dentro de este grupo diferenciamos:  

Nominativas: no existe ningún orden entre las categorías de variables. Por ejemplo: el grupo sanguíneo (A, B, AB, 0) o el color del pelo (moreno, rubio, pelirrojo).

Binarias: cuando toman dos valores posibles -si/no, presencia/ausencia- (por ejemplo: casado sí o no, tener el carnet de conducir sí o no).

Ordinales: existe un cierto orden entre las categorías de las variables, por ejemplo el nivel de estudios (sin estudios, básico, secundarios, etc) o categoría dentro de una empresa (peón, encargado, etc.)  

b) Cuantitativas: toman valores numéricos. Dentro de éstas se agrupan en: 

Discretas: tomas valores aislados, normalmente números enteros, por ejemplo número de hermanos o de hijos.  

Continuas: teóricamente puede tomar cualquier valor numérico por ejemplo: el peso de un individuo. Aunque en la práctica todas tomarían valores discretos por la imposibilidad de tener aparatos lo suficientemente sensibles para realizar mediciones intermedias.

La frecuencia absoluta es el número de veces que aparece un determinado valor en un estudio estadístico.

Se representa por f_i.

La suma de las frecuencias absolutas es igual al número total de datos, que se representa por N (es decir es el tamaño de la muestra):

f₁+ f₂ + f₃ + ... + f_n = N

Para indicar resumidamente estas sumas se utiliza la letra griega Σ (sigma mayúscula) que se lee suma o sumatoria:

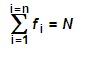
La frecuencia relativa es el cociente entre la frecuencia absoluta y el tamaño de la muestra.

La denotaremos por fr_i.

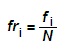
Donde N = Tamaño de la muestra. 

La frecuencia acumulada es la suma de las frecuencias absolutas de todos los valores inferiores o iguales al valor considerado.

Se representa por F_i.

 Los intervalos de clase se emplean si las variables toman un número grande de valores o si la variable es continua.

Se agrupan los valores en intervalos que tengan la misma amplitud denominados clases. A cada clase se le asigna su frecuencia correspondiente.

Límites de la clase

Cada clase está delimitada por el límite inferior de la clase y el límite superior de la clase.

Amplitud de la clase

La amplitud de la clase es la diferencia entre el límite superior e inferior de la clase.

Marca de clase (x_n)

La marca de clase es el punto medio de cada intervalo y es el valor que representa a todo el intervalo para el cálculo de algunos parámetros.

 

El diagrama de sectores o gráfico circular es un gráfico estadístico empleado fundamentalmente para variables cualitativas.

Las modalidades se representan en un círculo dividido en sectores.

La amplitud de cada sector, en grados, se obtiene multiplicando la frecuencia relativa por el valor 360º.

 

El diagrama o gráfico de barras es un tipo de gráfico estadístico que se utiliza para variables cualitativas y discretas.
En el eje x se sitúan:

• Las modalidades de la variable cualitativa.
• Los valores de la variable cualitativa discreta.

y sobre ellos se levantan barras cuya altura sea proporcional a sus frecuencias.

 

Un histograma es una representación gráfica de una variable en forma de barras.

Se utilizan para variables continuas o para variables discretas, con un gran número de datos, y que se han agrupado en intervalos.

En el eje abscisas (eje x) se construyen unos rectángulos que tienen por base la amplitud del intervalo, y por altura, la frecuencia absoluta de cada intervalo.

La superficie de cada barra es proporcional a la frecuencia de los valores representados.

MEDIA ARITMÉTICA: Se calcula sumando todos los datos y luego dividiendo este resultado por el número total de datos que tiene la muestra.

MEDIANA: Es el valor central de una serie de datos, para poder encontrar la mediana es indispensable que los datos estén ordenados.

 Para determinar la posición de la mediana se utiliza la fórmula (n+1)/2.

MODA: Es el valor que aparece con mayor frecuencia dentro de una muestra y es la medida más natural para describir datos.