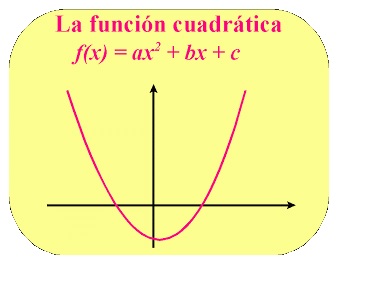
Matemática III
Gráfica
La gráfica de una función cuadrática es siempre una curva, o parte de una curva, que se llama parábola.
Los puntos del plano que verifican la ecuación y =ax2 + bx +c, con a distinto de 0 constituyen la gráfica.
Las parábolas son curvas que podemos descubrir observando nuestra realidad. En el siguiente video podes visualizar estas curvas en diferentes situaciones.
Elementos de una parábola
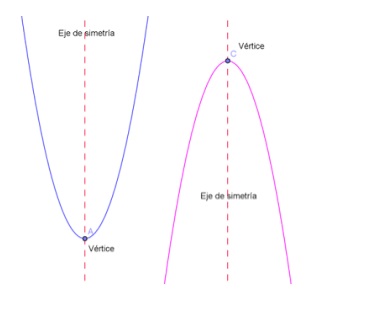
EJE DE SIMETRÍA:
Es la recta vertical que divide a la parábola en dos partes exactamente iguales. Para expresar el eje de simetría se escribe x = (punto de corte de la parábola con el eje x).
El eje de simetría de una parábola puede determinarse mediante la siguiente expresión:
![]()
los valores de "b" y "a" son los coeficientes de la fórmula de la función cuadrática.
VÉRTICE:
Es el punto donde el eje de simetría corta a la parábola. Se denota V(xv, yv).
Las fórmulas para calcular las coordenadas del punto del vértice son:
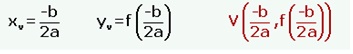
CORTES CON LOS EJES:
- Para encontrar los puntos de corte con el eje de las ordenadas (eje y), se reemplaza x = 0 en la fórmula y así se encuentra el punto (0, y).
- Para encontrar los puntos de corte con el eje de las abscisas (eje x), se reemplaza y = 0 en la formula, y luego se resuelve la ecuación de segundo grado ax2 + bx + c = 0.
Resolviendo la ecuación podemos obtener:
- Dos puntos de corte: (x1, 0) y (x2, 0) si el discriminante de la ecuación cuadrática es mayor que 0
- Un punto de corte: (x1, 0) si el discriminante de la ecuación cuadrática es igual a 0
- Ningún punto de corte si el discriminante de la ecuación cuadrática es menor que 0
NOTA:
Si no te acordás como se resolvían las ecuaciones de segundo grado haz clic aquí.