Ejemplos resueltos
El primer ejemplo permite a partir de la fórmula de una función lineal construir su gráfica.
En el segundo ejemplo se parte de la gráfica de una función lineal y se debe encontrar la fórmula (o ecuación de la recta) que le corresponde.
EJEMPLO 1:
Graficar las siguientes funciones lineales:
a) y = -3x + 4
b) y = 3
a) Grafiquemos de las dos maneras
1. Tabla de valores
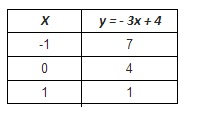
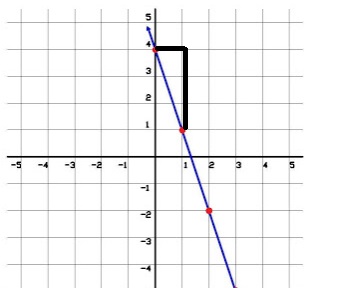
2. Pendiente y ordenada
Pendiente = -3
Ordenada al origen = 4
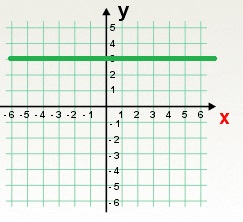
b) y = 3. En este caso el coeficiente que acompaña a la variable x es el 0. Esto quiere decir que la pendiente de la recta es 0 (no tiene inclinación).
EJEMPLO 2:
Dado el siguiente gráfico encontrar la ecuación de la recta.
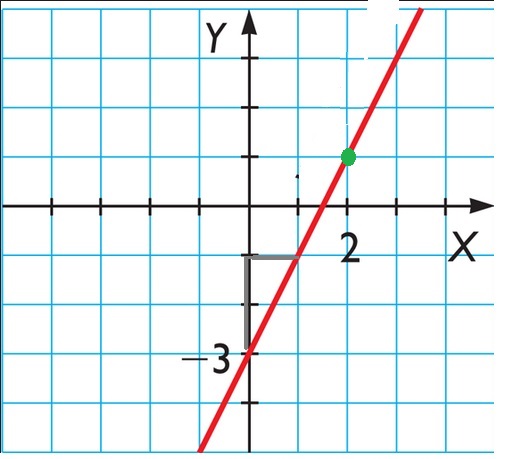
Con lo que hemos estudiado anteriormente sabemos que la fórmula que representa una función lineal es y = a.x + b. Por lo tanto debemos encontrar los valores de a y b para esta recta en particular.
Como vemos en el gráfico la recta corta al eje y en -3, por lo tanto este es el valor de la ordenada al origen (b), al reemplazar este valor en la fórmula queda:
y = a.x - 3. (*)
Ahora nos falta encontrar el valor de a, es decir el valor de la pendiente. Para hallarlo tenemos dos maneras:
1) Buscamos otro punto que pertenezca a la recta dada, por ejemplo (2,1). (en el gráfico aparece marcado en verde)
Ahora reemplazamos las coordenadas del punto en la ecuación (*)
1 = a.2 - 3 -----> Si recordamos las coordenadas de un punto son un par ordenado (x, y), es decir el primer valor corresponde a la x y el segundo a la y. Por eso se reemplazo en la igualdad la x e y por los valores 2 y 1 respectivamente.
Ahora debemos "despejar" la letra a
1 = a. 2 - 3
1 +3 = a. 2
4 = a. 2
4 : 2 = a entonces a = 2. Luego la ecuación que buscamos es y = 2.x - 3
2) Otra manera es recordando como se explicó la segunda manera de graficar utilizando pendiente y ordenada al origen.
En la fórmula y = a.x + b , el valor de b = -3 y el de a = 2 ( ya que a partir de la ordenada se tomaron dos unidades hacía arriba y una a la derecha).
Por lo tanto la fórmula es y = 2.x - 3